OK, so here goes. This technique is sortof a poor-man's Sigma-Delta converter, but with a moving window average filter instead of a sinc filter (for good reason!).
For the sake of discussion, lets assume a nominal PWM frequency of 18 kHz. Its a pinch faster than some of the existing available drives, slow enough to control with a reasonable gate drive, and near the limit of human hearing, typically on the inaudible side of that limit. So it should be in the ballpark.
The hard part is that a 1.4 khz line freq (~80k erpm) is barely one decade less than the pwm frequency. And there is a ton of noise at the pwm freq and its harmonics. Mostly odd harmonics, but there will be some even harmonics, too at any time the duty cycle isn't exactly 50%. My idea is to use four mechanisms working together to eliminate the noise, while still allowing for a very fast fault current detection.
First, if the pwm carrier is an up/down-counting triangular wave (as opposed to a sawtooth), with synchronous rectification, then the motor's ripple voltage and current are actually at 2x the pwm silicon frequency. Assuming a trapezoidal drive pattern for the moment (SVPWM is similar), the switching sequence goes:
(leg, leg, motor volts), where leg == 1 for high switch on, and 0 for low side on, B is battery voltage
(1, 1, 0) -> (0, 1, B+) -> (0, 0, 0) -> (0, 1, B+) -> (1, 1, 0).
While each phase leg follows the sequence 1->0->1, with only one falling and one rising edge, the motor saw a pair of B+ and a pair of 0 voltages. So, you have effectively doubled the motor's voltage frequency, halved its ripple current, and stretched the gap between f_line and f_pwm by a factor of 2.
Second, oversample the motor current and perform a simple average over the results. The advantage here is an exact harmonic cancellation of the ripple current and its first few harmonics. For an N-th order moving window average, the first harmonic to be canceled is f_oversample/N. The first non-cancelled frequency will be at f_oversample, which will appear as DC. Above a certain threshold, non-harmonic switching noise will be a major factor. So, why do you care about all this noise? Everything above the nyquist frequency of your control loop will alias in if you don't filter it out. PWM ripple current will be the dominant source of noise up to a point, and then switching noise will be a factor.
Third, place a two-pole analog Bessel filter in front of your ADC. Why a Bessel filter, and not a Butterworth filter? Because the butterworth filter is not minimum-phase or linear phase, and phase delay at the line frequency will be a serious problem for closed-loop control. Why 2 poles? Because its easy to get 2 poles with just one opamp, and I don't think you need many more than that. You can estimate what the noise level of that N-th order harmonic will be, and stamp it down to less than the detectability of your ADC. I'll just leave the mathematics behind that decision to the GNU Octave script that I attached.
Given the following nominal parameters:
f_line = 1.4 kHz
f_pwm = 18 kHz
N_oversample = 6
N_poles = 2;
L = 10 uH inductance (just about the worst we can imagine right now)
V = 72 VDC
10-bits of (pwm-) noise-free current measurement
400A full scale current sensor
The attached script places a two-pole Bessel filter at 33 kHz, with only 11 degrees of phase delay at f_line, and > 10 kHz of usable bandwidth. This is the Bode plot of the total filter's transfer function.
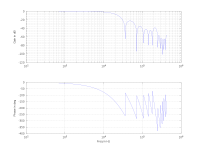
The slightly higher hump at ~200 kHz is the first uncanceled harmonic, which aliases in as DC. The low-pointing spikes in the gain plot are the canceled harmonics. Everything higher than the first negative spike will alias in, but -48 dB is the threshold of detection for a 10-bit ADC. Don't read anything into the depth of those spikes, they are effectively infinite for a digital filter.
Fourth, route the un-filtered original signal to a pair of analog comparators for fault detection, because that's about the only way you can get fast enough to save the 'fets. I'll try to get a schematic of the analog filtering circuits up later, but it may be a few days before I can get a free round tuit.


