Conclusive proof gearboxes are awesome.

[Teh Stork]

Gearbox, no gearbox has had a debate with little proof and a lot of anectdotes flying wildly. In this example I will show you how implementing a gearbox can increase system efficiency and power.

First things first, some measures of energy, power and rotation.

Disclaimer: I'm european so I do 0,5 instead of 0.5, and SI units.

Energy stored in kinetic energy: 0,5*mass [kg]*velocity^2 [m/s] (^2 means squared).
Rotational power: Nm*Omega (angular speed). [Rad/s] (often confused with angular frequency).
RPM=Omega[Rad/s]*60/2*Pi.
Omega[Rad/s] = RPM*2*Pi/60

Then, imaginary motor data:
Motor resistance: 100mOhm.
Torque per amp: 1,1 Nm/A
Max Rpm: 500
Max Rad/s = 52,3

Motor losses:
Parasitic losses approximated to 2W per rad/s. (Bearing and Hysteresis losses).
Copper losses: I^2*R (R i is motor resistance).

Parasitic losses: Taking these into account is in disfavor of the gearbox connected motor. They won't make a huge difference, but taking all things into concideration, they need to be taken into account.

Gearbox:
Three speed.
1:1 70km/h at 500RPM
1:1,50 46,6km/h at 500RPM
1:3 23,3km/h

This was 'designed' by taking the whole gear range and dividing them by three. There might be more efficient ways to do this, taking into account kinetic energy scales by the square.

Bikes:
With gearbox: 110kg
Without gearbox: 100kg

And so it begins, gogo: lets see who reaches 70km/h first.
Energy @ 70km/h gearbox bike: 20700J
Energy @ 70km/h non gearbox bike: 18800J

Challenge: accelerate as fast as possible to 70 km/h. 70km/h = 19,4 m/s. We run 50A to the motor, giving us a steady 250W losses and 55Nm from the motor. This is the result:


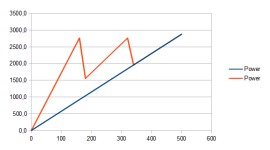
In red: gearbox.
X-Axis: Wheel RPM
Y-Axis: Power

For those extra interested, power calculations are done in Openoffice Calc - the file is added. Look through all the sheets. I've modified torque for the calculations, but modifying rad/s would net the same result.

Power is one thing, what is more interesting is acceleration. To do this we find the mean power value, based on this - we can take energy and divide by mean power - giving time. The non- gearbox solution is easy. Half of 2880W is 1440W. 18800J/1440W equals 13 seconds. Parasitic losses (mean): 50W*13s=650J. Active losses (mean): 250W Total losses: 3900J. Total efficiency:18800J/18800J+3900J = 82,8% Total energy: 22700J

The gearbox solution is harder, mean is found by taking the average of all the samples and dividing by the sample amount. When I do this in Calc, I get 1980W average. 20700J/1980W equals 10,5 seconds. Parasitic losses (mean): (1,6s*50W+3.16s*77W+5,74s*86W)= 828J. Active losses: 250W. Total losses: 3330J Total efficiency: 20700/20700+3330=86,1% Total energy: 24030J

Calculations for individual gears:
Energy @ 23,3km/h: 2302J Mean power: 1440W. Time in gear: 1,6s
Energy @ 46,6km/h: 9215J Mean power: 2190W. Time in gear: (9215J-2302J)/2190W = 3,16s

That was the boring half of the story - here is the fun part that is closer to reality aswell. How long does the bikes use to 46,6km/h? (making calcs easier )

Gearbox model: 4,76s (1,6+3,16)
Non-gearbox model: Mean power: 975W. Total energy: 8380J. Total energy/power = 8,6s

Now look at that difference. The gearbox model clearly offers much better performance.

Observations regarding this model:
1. Gearbox bike is disfavoured when it comes to weight.
2. Gearbox bike gearbox efficiency is not calculated in.
3. Power graph gear changes is a bit sloppy modeled.
4. Total energy to get both bikes up to speed is lower in the gearless bike, but this is much due to nr 1.
5. Gearbox bike absolutely owns gearless bike in acceleration test.
6. The imaginary motor model is very real, but the whole system with inverter is kept out of the equation. If added, gearbox bike would benefit.
7. Both motors are run under peak efficiency point (@88%)(witch is about 16A phase for just under 18Nm).
8. A gearbox solution greatly improves efficiency.

Observations regarding gearboxes:
1. If you have too much torque off the line, a gearbox will be no good.
2. An induction motor is, due to non-fixed V/f characteristic, not similar to a permanent magnet motor(hereafter PMM). (Tesla motors anectdote).
3. "Electric torque" is less "peaky" than ICE torque.
4. Several speed gearboxes on ebikes are very rare (is there any purpose built?).
5. If you had "infinite gears", mean power would be doubled from a PMM.
6. A gearbox allows the motor to spin faster so that the motor does not need to have same phase amps (biggest source of loss during accel).
7. A gearbox solution greatly increases low range performance.

Please don't turn this post into another gearbox shitfest. I might have commited blunders and I'd ideally like to use more time on this post, but I don't have the time to(many calculations is missing - but I've tried adding them where there could be confusion).

About the overly arrogant title, yep - that's typically me (I've been wrong more than one time, it's nothing new - but self-confidence in the field is just a bit too high ): Just know I'm sincere when I say I believe they've earned the title

Edit: Fixed image (X-axis was off.)

 

[Lebowski]

Same here, I think arrogance is a good quality to have as an researcher / engineer. It gives me confidence, believing that I know best and the rest of you
are a bunch of blabbering idiots. It makes me question the status quo and go onto new and previously undiscovered paths.. Sometimes you run into a brick
wall but other times you are able to build new and totally awesome stuff nobody else has 8) . This is how technology advances (especially when I want to
rub it in and tell you all about how my stuff works, also known as 'publishing in the literature').

About gear boxes, during the build of my motor V1 I concluded you get the most mechanical power for your electrical power
when the motor is spinning fast (high V -> low I -> lower resistive losses -> more mechanical power). And more mechanical power
equals more accelleration. To keep the motor spinning fast at all speeds you need a gearbox. That's why motor V2 is going to
be used as a mid drive and the rear gear cluster on the bike will be my gearbox. And why my GF has a bosch mid-motor ebike and
not a rear-hub type.

 

[Miles]

2. Gearbox bike gearbox efficiency is not calculated in.

You'd have to do that and work out the overall efficiency for a specific usage pattern, before you can make any claim as to which is the most efficient (GB or no GB), in what circumstances....

 

[alan]

Yes, the gear shift modeling is sloppy. In reality, during the time of the shift, there is zero power, and the wheel speed will be decelerating. That means the downslope shown in the graph for the gearshift should be down and to the left, not to the right. Even if the tranny can shift in a split second, you still need time for the motor to decelerate, and to minimize jerk (the third order rate of change) that could otherwise cause a loss of traction on the road, so proper modeling of each shift may be very significant to this analysis.

-- Alan

 

[liveforphysics]

Your losses aren't modeled correctly.

Also, if your motor isn't saturating, you could simply increase phase current to replace the transmission with something that doesn't add parasitic friction and weight and have the same or more area under the curve.

 

[Ypedal]

add to the above comments, a 10kg gearbox ? .... at 3kw peak ? lol..

 

[Teh Stork]

Your losses aren't modeled correctly.

Also, if your motor isn't saturating, you could simply increase phase current to replace the transmission with something that doesn't add parasitic friction and weight and have the same or more area under the curve.

Enlighten me as to what is missing from the loss analysis. Even if the motor isn't saturating, increasing phase currents make for terrible efficiency.

add to the above comments, a 10kg gearbox ? .... at 3kw peak ? lol..

The big weight was partially to make up for the fact that the shifts weren't modeled thoroughly. 3kW was to make it somewhat bikelike.

In light of these comments I should shed ligth on the fact that I neglected inertial forces and losses while shifting, but they're really not that big.

Miles: I agree with you that usage pattern is important, but I chose to neglect gearbox losses as they're in the 98-99's.

 

[liveforphysics]

Your losses aren't modeled correctly.

Also, if your motor isn't saturating, you could simply increase phase current to replace the transmission with something that doesn't add parasitic friction and weight and have the same or more area under the curve.

Enlighten me as to what is missing from the loss analysis. Even if the motor isn't saturating, increasing phase currents make for terrible efficiency.

It actually improves efficiency up until the the point core loss equals copper loss, then efficiency starts to go down, but when starting from a stop, as in zero rpm making torque, both efficiencies start at 0% (because there is no RPM when stopped, just a torque force), and then begin to move towards a non-zero efficiency. The transmission motor can move away from zero% efficiency sooner, but also arrives at increased core losses sooner, as well as suffering the additional frictions and weight and complexity of the system. The direct drive option, if given the thermal path to deal with the relatively minor extra heating to match the acceleration performance through additional phase current while starting out can match and exceed performance and efficiency due to reduced shifting time delays and weight/friction etc.

In other words, if you apply the same weight/volume/space/cost the transmission occupies towards your motor growing in radius, you not only improve system efficiency and reduce complexity, but it's also the ultimately highest possible cruising system efficiency and will have a larger continuous power capability due to the motor being larger.

 

[Lebowski]

how about with a CVT transmission designed to keep e-motor rpm contant independent of vehicle speed ? Like for instance in those 125cc Vespa scooters ?

 

[Miles]

Miles: I agree with you that usage pattern is important, but I chose to neglect gearbox losses as they're in the 98-99's.

It's a 10kg derailleur?

 

[Miles]

how about with a CVT transmission designed to keep e-motor rpm contant independent of vehicle speed ? Like for instance in those 125cc Vespa scooters ?

Like I said. What's the continuous loss from the variable transmission itself, against the periodic gain from having it?

 

[liveforphysics]

how about with a CVT transmission designed to keep e-motor rpm contant independent of vehicle speed ? Like for instance in those 125cc Vespa scooters ?

If you were a gas engine, I could definitely see needing one and having it be a huge advantage in many ways (the reason they are so prevalent). But for a properly sized electric motor, I can see nothing but higher system efficiency, highest reliability, lowest weight, lowest cost by designing the motor to be already turning at the right speed you wish to be cruising along at most efficiently and not making your power go through various other transfer stages, each one taking it's tax in friction and heating and wear and weight and noise etc, just to end up where you could have been from picking a motor made to run efficiently at the speed range you can use something simple like single stage direct drive with.

Doesn't quite make sense IMHO even at a high-level conceptual overview, let alone when you work the numbers out comparing the two systems. The possible exception being if you're trying to make the most of some cheap common available motor that isn't well suited towards your application to begin with, but you can apply band-aids like transmissions to try to overcome it's weaknesses in your application at the cost of expense and complexity etc.

 

[Rassy]

how about with a CVT transmission designed to keep e-motor rpm contant independent of vehicle speed ?

There was a previous discussion about this. In my case I run my motor at a higher RPM where it is in it's efficiency zone instead of it's torque zone. It has just enough grunt left to reach the next shift point when accelerating on level ground. My auto shift CVT is set up with 11 ratios that keep the motor spinning between 180 RPM and 210 RPM. The motor is a slow wound 9C clone 6x10 with a 48V battery on a trike with a gross weight over 300 pounds.

Initially I tried to run it with the shift points set at a higher RPM, and as the speed increased it reached a point where it could no longer pick up enough speed to shift into the next gear without serious pedal input. I've never tried setting the shift points under 150 RPM, but I expect it would have better acceleration until it reached 180 RPM in high gear, at which point it would be the same as it is now.

Since I wanted good hill climbing and maximum efficiency for long rides, I am very happy with this setup. Once the hill reaches about 20% grade it will shift into low gear and again there's no way to improve the low gear performance by changing the other shift points.

Anyway, more to the point, since an electric motor produces it's maximum torque at stall, I don't think any gearing system would out accelerate a properly sized direct drive system. It's just when you start including other issues, such as efficiency, heat, distance, hill climbing, etc. that the gearing system has merits.

Note: LFP pretty much said the same thing while I was typing this, and I agree. My 6x10 9C motor would soon burn up on the hills if it was used as a hub motor as intended unless it was modified. The CVT works great for my slow speed needs.

 

[liveforphysics]

how about with a CVT transmission designed to keep e-motor rpm contant independent of vehicle speed ?

There was a previous discussion about this. In my case I run my motor at a higher RPM where it is in it's efficiency zone instead of it's torque zone.

This is the misconception. That "efficiency" zone is more efficient from a motor to energy conversion perspective, but from a net system efficiency of pushing the bike forward, adding more phase current and keeping motor speeds down (so BEMF is very low) requires very little energy out of the battery, and while it's using the power inefficiently, it's really a very small amount of power that it's using to begin with (at least for controllers with phase-current limiting rather than just battery current limiting.)

 

[liveforphysics]

I think the better way to look at it from an efficiency perspective, is that the copper loss % is identical when you're dumping in max phase current (say 100A or whatever) when the rotor is stalled vs when the rotor is at say peak efficiency RPM at like 4,000rpm or something. You pay the exact same copper loss price in energy lost to make that same 10ft-lbs of torque or whatever, you just also are paying a bunch of extra core loss energy taxes now as well, and due to the nature of the relationships it causes one to be 0% efficient (when rotor is stalled) and one to be 95% efficient (or whatever), yet in reality to put 10ft-lbs on the rear wheel to take off from a stop (or whatever you were looking to do), the direct drive one just trades core loss for copper loss, which is actually quite a minor loss for many applications.

 

[gwhy!1]

I was never in a position to test efficiency of a cvt if used with a electric motor but I would like to say that I really dont think that a motor on its own could out perform a well setup cvt for the power input. I really cant imagine any motor on its own running on 48v at a 75A limit run a 55kg scooter upto 36mph in just a little over 5secs , the scooter could also be wheelied from a standstill ( with very little persuasion ) it would also go up any grade you pointed it at and this was with all less than 4kw of input .

 

[liveforphysics]

75A battery current can be 750A motor current very easily.

You would be surprised what a motor can do in handling bursts of over-current, and the torque it makes as a result.

 

[Thud]

The only time it makes perfect sence is under constraints of a motor topology....or if your dealing with extreams in aplication...such as a mountin climb in the middle of your flat land high speed comute.

if you can just motor up & carry a mongo battery pack, you would have no justification for the added weight & complexity.
Top fuel cars have no issue running one gear ratio.....

I know the tiny 50mm motor in my 1st bmx wouldn't of had 1/2 of the performance envelope without the 2 speed.
It's conclusive!

 

[liveforphysics]

if you can just motor up & carry a mongo battery pack, you would have no justification for the added weight & complexity.

You can motor up, and carry a slightly smaller battery pack, because your system efficiency will higher with properly done direct drive than is possible with a transmission over like 90% of operating ranges.

It really is just those bizarre fringe applications where your commute consists of half towing a dump-truck up a hill at 0.1mph or something, and the other half cruising along the highway at 40mph under light loads or whatever are what it requires before a transmission makes a net efficiency advantage IMHO.

For ultimate purpose-built EV bike/motorcycle performance or EV performance etc, a transmission will never have a place

 

[flathill]

My 6x10 9C motor would soon burn up on the hills if it was used as a hub motor as intended unless it was modified

Ah but that is a whole different topic..direct drive hub/wheel motors with no leverage at all
only thing you can do is grown the diameter or make it wider

You do need a single speed fixed gear(box) or chain/belt reduction in most applications for sure
the Tesla: "single speed fixed gear with 9.73:1 reduction ratio"
The Zero motorcyles are around 5:1
You just need more volts to make the motor spin faster for high top speed
with a big enough motor at low speeds you are going to hit traction and wheelie limits before you need more gear or saturate the motor
Note the Tesla has ceramic bearings 8)
the argument we are having here is single speed vs multi speed gearboxes

you can even have a two stage reduction but still be single speed
the BRD motorcyle motors spins insanely fast
straight cut gear in oil bath first stage (noise on purpose + efficiency)
second stage chain

 

[xenodius]

So, I'm a huge lurker, and I have to get this question out. It may be a really stupid question, but relates to efficiency and "gearing" in general, along the lines of what flathill said.

Wouldn't the most efficient ebike be one which runs a low Kv hub-motor at high voltage in a relatively small wheel? Wouldn't this motor have greater power output with less resistance losses? I understand that "iron losses" (eddy currents, right?) are a problem at much higher speeds, (Also heard current saturation thrown around?) and there's always an efficiency zone with hub-motors, but assume you don't hit that ceiling. Isn't the current what ultimately results in heat generation, not the voltage? If you can get the same speed out of higher voltage, you don't have to push as many amps to get the same power... right? Kind of like what flathill is saying-- high-voltage reduction systems. But without the reduction system.

And a second question. Aside from the setup difficulty, why not use a robust series/parallel switch (or... several?!) in the phase winding to alter the Kv of the motor? Or even split the battery pack and halve the voltage? I suppose only the first case would allow for real on-the-fly gearing changes, what with the controller shutting off in the second case, but still. Is there a flaw with this?

I envision the ultimate EV running on an electronically "geared" (Kv switch), well-made direct-drive BLDC motor and a high-voltage field-oriented controller. Why would a mechanical transmission ever be considered if an electronic one of negligible weight, maintenance, and efficiency was at all possible?

I'm not being sarcastic at all, I'm genuinely curious and I want someone to poke holes in my bubbles because I'm certain they're too good to be true.

 

[amberwolf]

It really is just those bizarre fringe applications where your commute consists of half towing a dump-truck up a hill at 0.1mph or something, and the other half cruising along the highway at 40mph under light loads or whatever are what it requires before a transmission makes a net efficiency advantage IMHO.

So something like my situation where I:
-- normally ride short 2-3mile commutes on flat roads with a dozen or more stops, WOT from a stop until 20MPH, cruising there until i approach a traffic control and coasting down or braking,
--sometimes hauling cargo making the overall weight total 500lbs+
--sometimes riding long hauls of 10-20 miles with very few stops (same throttle/speed/brake pattern)
--sometimes riding long hauls that include slow increasing grades over several miles of it, then down the other side (Greenway Road around North Mountain)
--sometimes the grade is pretty steep for short or long sections (Cave Creek Road on North Mountain)

A transmission seems to me to make sense in this situation--although a hubmotor (even just my 2807 9C in a 26" wheel) works fine for all the above situations so far. I have a BLDC powerchair motor
http://www.endless-sphere.com/forums/viewtopic.php?f=30&t=32838
intended for 24V operation at RPMs that would give either 4 or 8MPH in a 14" wheel (I can't remmeber which wind it has). I'm intending to run it (at least at first) with either 10s TS60Ah cells I have, or a bunch of RC LiPo series/paralleled for perhaps a slightly higher voltage. Then drive either a 3-speed Sachs IGH or more likely a NuVinci 171 Devkit, driven so that I can hit a 30MPH top speed (which probably will never see any use outside of a racetrack but will help me GTFOOTW of idiots by being *able* to go faster quickly if needed), cruise at 20MPH, and accelerate very quickly from a complete stop even with heavy cargo. (which I am hoping to be able to be at least 500lbs capacity plus the 300lbs bike and me)

Does it make sense to use a transmission in such a case?

 

[flathill]

For hauling heavy loads you want a multi speed
Here in the valley a stealth startup is working on an awesome
clutchless gearbox
The speed sense accuracy is so great it can mesh the gears no synchro
Ian Wright
The real Tezla founder

200hp contin 400hp 10 seconds

sSimulated Truck Acceleration, Full Torque Stop
1. Motor is accelerated to 20,700 rpm in first gear
Upshift (Shift from 1st gear to 2nd gear)
2. Motor torque is reduced to zero
3. Shift actuator is moved to neutral position (mid-stroke)
4. Motor speed is synchronized to the correct speed for second gear, 9000 rpm (80 ms)
5. Shift actuator moves to second gear
6. Torque is reapplied to maintain "vehicle speed"
Downshift (Shift from 2nd gear to 1st gear)
7. Motor torque is reduced to zero
8. Shift actuator is moved to neutral position (mid-stroke)
9. Motor speed is synchronized to the correct speed for first gear, 20,700 rpm (80 ms)
10. Shift actuator moves to first gear
Full-Torque Traction Drive Stop
11. Motor comes to full stop

[youtube]TXQGw7S-xOU[/youtube]

 

[liveforphysics]

For hauling heavy loads you want a multi speed

Is it? I was under the mistaken assumption you just wanted the torque at the wheels that you require to move your heavy load.

You do realize the things that move the most heavy loads on earth, freight trains, are entirely single-speed electric drives right?


I think a big misconception in this thread, is that you get some magic trick of using less power if the motor is spinning much faster. The reality is, the least amount of energy you're going to use to create a given torque from a motor will be the lowest RPM you can create this torque you require at.

 

[neptronix]

The reason we don't have transmissions is simple economics.
Electric motors are cheap, batteries are very expensive.

Oversizing a motor for the task does not give you an efficiency penalty, or really, much of a weight penalty.
When we see motor prices go upwards, you will start seeing transmissions become more common.