Analysis of regen on an ebike

[justin_le]

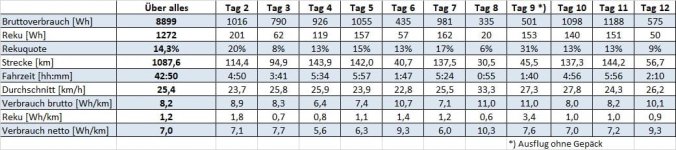
Excellent thread, especially start and end, now understanding quite a bit more on regen efficiency, but given the tradeoffs of various systems in term of hill-climbing efficiency, I would appreciate your insights on the overall performance in a mountainous area. The irony is that while it is arguably the most sensible use environment for regen use (both in term of regen and lower brake wearing), it is also where mid-drives or geared motors are typically recommended since they work at maximum efficiency. Hoping to get Justin involved in this, I'll start quoting ebikes.ca (https://www.ebikes.ca/product-info/grin-kits.html#geared-vs-direct-drive):

- Pros of Geared Motor: Better hill climbing efficiency
- Pros of Direct Drive: Regenerative braking

(I understand that mid-drive would stand there as: Even Better hill climbing efficiency -- whatever that means)
You will agree that for whoever wants to purchase his/her first ebike, that is confusing : )

Hi Mahe and thanks for re-engaging with this conversation, it's one of my favorite subjects too!
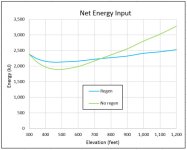
The generalization that geared motors are more efficient than DD for climbing hills is only true when comparing motors that are in the same nominal power category. A large direct drive motor like the BIonX D can climb hills with better efficiency than most of the geared hub motors on the market. Here it is more efficient across the entire speed range compared to the extremely common Bafang G01 hub.
https://www.ebikes.ca/tools/simulator.html?motor=MBionxD&grade=8&cont=cust_40_40_0.01_V&cont_b=cust_40_40_0.01_V&motor_b=MG01_STD&grade_b=8&bopen=true

So it's not really a question of being geared or not. What makes for an efficient hill climbing motor is having a relatively low winding resistance for the motor kV so that the I^2R copper losses at large torque levels aren't too high, and a geared drive an achieve that with a much smaller motor size. Here's a comparison of the eZee motor and a 9C style DD motor when both are normalized to have the same kV (8 rpm/V) and running a constant 40 amps of phase current. This is the kind of comparison that results in a generalization of higher hill climbing efficiency for geared motors since they're both hubs that would normally be considered in the same power class:
https://www.ebikes.ca/tools/simulator.html?motor=MEZEE250&grade=8&cont=cust_40_40_0.01_V&cont_b=cust_40_40_0.01_V&motor_b=M2707&grade_b=8&bopen=true



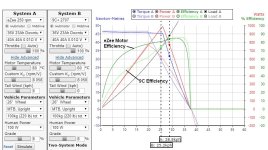
The eZee motor has a winding resistance of 75 mOhm, while the 9C motor when wound for the same RPM/V is more like 230 mOhm, so about 3 times higher copper losses for a given torque production.

Can you give any number on that? Even theoretical.

Very happy to do so!

The trick is not to use the motor simulator which only shows the steady state curve of a motor output, but instead use the trip simulator web app which allows you to plot a time evolving simulation of an ebike travelling over any arbitrary terrain that you can draw (or load from google maps). We've just recently updated it so that it encodes the simulation parameters in the URL which will make showing this really easy. As a random example, let's take the same 9C DD motor and go up and down a hill, 400m elevation climb over 14km with a ~7% grade.


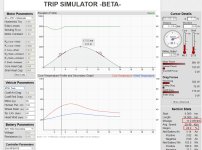
With regen enabled and a 40 kph speed limit riding in a tuck position, we use 11.2 wh/km and get about 22% regen doing the trip in 21min 13sec (screen capture above taken with slightly different parameters than URL link):

https://www.ebikes.ca/tools/trip-simulator.html?m=M2707_SA&v=cust_ad0.4_rd0.008&ms=90&h=100&w=26&sp=40&wv=0&b=B5216_GA&c=cust_pl75_rl75_bl25_cr0.02&rg=true&t=21&ct=21&st=21&i=evd&s=st&p=16A08862FN9V

Meanwhile, if the speed was limited to 30 kph instead of 40 kph, then you'd get an amazing 56% regen and use just 7.3 wh/km in 27m 52s
https://www.ebikes.ca/tools/trip-simulator.html?m=M2707_SA&v=cust_ad0.4_rd0.008&ms=90&h=100&w=26&sp=30&wv=0&b=B5216_GA&c=cust_pl75_rl75_bl25_cr0.02&rg=true&t=21&ct=21&st=21&i=evd&s=st&p=16A08862FN9V

So those are some benchmark numbers for a regen enabled system using a generic direct drive hub motor, with both 40kph and 30kph cruising speeds.

Now lets compare this to a mid-drive BBS02 system. Here it doesn't make sense to compare in the same manner where we go up and down the hill at the same speed since that's not how you'd use a mid-drive. What we want to do is climb slowly in a nice and friendly gear, and then on the downhill stretch where there is no means of recapturing regen energy we go as fast as the hill allows, and to be fair we need to choose that climbing gear such that the total trip time is the same as with the direct drive motor. Unfortunately we haven't yet implemented a 'motor freewheeling' feature in the trip simulator so for now we'll divide the trip into the uphill and downhill sections.

To simulate freewheeling on the downhill stretch, I've put a motor phase current limit of just 2 amps, and from the 7.5km point to the end we cruise down pretty fast averaging 52 kph taking a total time of 7min 28 sec:

https://www.ebikes.ca/tools/trip-simulator.html?m=M2707_SA&v=road&ms=90&h=100&w=26&sp=70&wv=0&b=B5216_GA&c=cust_pl1_rl30_bl25_cr0.04&rg=false&t=21&ct=21&st=21&i=evd&s=st&p=16A08862FN9V&x=&y=&lx=591&rx=487&rw=700

Then here comes the fun bit, which is figuring out how most efficiently to do the hill climbing half using the BBS02 such that we end up with the same average speed as the previous sims with the DD hub motor. To compare against the 40kph case with the DD hub, we need to do the climb in 21m 13s - 7m 28s = 13m 45s, and find the effective gear ratio that will achieve this, which we can do using the "run simulation set" feature. Here we're simply varying the wheel diameter since there isn't a separate "gear ratio" input yet for mid-drives but changing the wheel size has exactly the same effect


With the resulting data plotted we see that a wheel size of 51 inches gets us the hill climb in the target 13.75 minutes, so that our total trip time up and down the hill is 23 mins 24 sec, same as with the DD motor and regen.



https://www.ebikes.ca/tools/trip-simulator.html?m=MBBS02&v=road&ms=90&h=100&w=51.3&sp=40&wv=0&b=B5216_GA&c=cust_pl75_rl75_bl25_cr0.02&rg=true&t=21&ct=21&st=21&i=evd&s=st&p=16A08862FN9V&x=&y=&lx=0&rx=238&rw=487

The net result is that the hill climb with the BBS02 motor geared optimally for 13min 45 sec requires 148.2 Wh


Over the full trip including the downhill coast, that works out to be 148.2 Wh / 13.9km = 10.6 wh/km, which is in fact a bit better than the DD motor with regen (11.2 Wh/km). So in this particular example the regen gained on the downhill portion doesn't _quite_ compensate for the reduced motor efficiency while climbing, and the mid-drive setup has better net mileage.

On the other hand, if we used a more efficient GMAC motor instead of the generic DD hub motor, then the that same trip uses 10.3 wh/km and gets 25% regen
https://www.ebikes.ca/tools/trip-simulator.html?m=GMAC10T&v=cust_ad0.4_rd0.008&ms=90&h=100&w=26&sp=40&wv=0&b=B5216_GA&c=cust_pl75_rl75_bl25_cr0.02&rg=true&t=21&ct=21&st=21&i=evd&s=st&p=16A08862FN9V

In this case it gets better mileage than the BBS02 mid-drive.

You can use this method to play "what-if's" on all kinds of scenarios, and find all kinds of hill grade and speed situations where a particular mid-drive motor has better net efficiency, and all kinds of situations where a regen capable hub motor has better net efficiency. There isn't a simple rule of thumb answer. But my own observations both analytically (like the above example) and empirically is that most of the time a well optimized regen setup (like the GMAC + Phaserunner) generally has an edge over a mid-drive like the BBS system when riding in hilly terrain.

 

[Cephalotus]

Here is some practical experience from driving a BionX D series speed pedelec in Switzerland and France.

Bike weights around 25kg (incl water and lock), luggage around 15kg (depending on water and food) and my own weight is aroudn 80kg. battery was a 13s8p Panasonic PF pack.



Amount of regen.

I calculate that with regen= energy regenerated / energy consumed which is industry standard and different frm the cycle analyst calculation.

14,3% may not sound so much but keep in mind that with speed pedelecs power consumption is significantly higher than with 25km/h pedeles, so regen is much lower. Regen helped to finish some days, because otherwise the battery would not have lasted.

On day 10 and day 11 some amount of recharge from the grid was done during the trip.

Day 9 was riding up an hill, going hiking and later going down the same hill.



More detailed power consumption:

 

[markz]

I like the way the Trip Simulator has been updated.
Input mode easy to find at the top of the graph/map.
Google Maps auto geo-locates the ip address - used to always zoom out from Van, then move the map over on province then zoom in.

.

 

[osa57]

Hi,
Concerning this subject, here I would like to bring some concrete results of real life tests on a more specific point:

Is there any relationship between:
- amount of energy recuperated by regenerative braking
- speed of the bike in the descente

In order to discuss above relationship I have performed the following test:

- maintain the maximum speed in a given descente below a given limit in km/h
- at the end, measure the amount of energy (Ah) that has been regenerated in above section

I am using a 9C RH212 DD with a 52V 28Ah battery and a Phaserunner controller.
Total weight (rider+bike)= 110kg

I have been able to reach these conclusions:

1) The speed at which the regenerative braking produces more electricity is 25 km/h with 0,51 A/h [best case in this test set] : this is slightly more than with 20 km/h max speed (0,50 Ah)
2) With higher speed by using regenerative braking we recuperate less energy: at 40 km/h we have produced 'only' 0,26 Ah [worst case in this test set]
3) Increasing speed from 25 km/h to 40 km/h represents a "regen loss" of 50%!
4) Similarly if we increase speed from 25 km/h to 30 km/h, this represents a "regen loss" of 17%, while from 25 km/h to 35 km/h we have a "regen loss" of 27%
5) When we compare the results from previous set of tests (performed WITHOUT any fairing) we see significant improvements :
> At 25 km/h from 0,43 Ah to 0,51 Ah
> At 30 km/h from 0,39 Ah to 0,42 Ah
> At 35 km/h from 0,3 Ah to 0,37 Ah

If you are more interested you can have a look at my web site where I have more details:
http://gonano.eu/regenerative-braking-efficiency
http://gonano.eu/regenerative-braking-efficiency-versus-speed-part-two

regards
Daniele

 

[thundercamel]

I'd say that makes sense. More energy is being lost to wind resistance instead.

 

[justin_le]

Concerning this subject, here I would like to bring some concrete results of real life tests on a more specific point:

Thank you Daniel for posting this and I'm always grateful to see real world test data coming in to either validate or disprove things that are predicted by the models. The case of optimal regen speed on the downhill for maximum data recapture very much mirrors the case of finding the optimal hill climbing speed to minimize consumption. If you go too fast you loose too much energy to wind resistance, and if you go too slow you waste too much energy to motor heating. (If motors had no winding resistance, then the optimal speed would be very slow).

What's interesting here is that your results almost exactly match the same conclusion that I got for finding the optimal hill climbing speed in a typical setup. You can see that around the 1hr 10 minute mark of the motor efficiency presentation here:
https://youtu.be/dxJe_gygRGU?t=4282

In that case I found that with a direct drive hub motor climbing a 6% grade hill, optimal speed for a regular bike was about 18 kph while for a velomobile it was 26 kph.

 

[Lebowski]

good chance that the regen is not implemented correctly for max efficiency... regen should be done with Stator Oriented Control for max energy recuperation, not with Field Oriented Control.

 

[justin_le]

Do elaborate Lebowski! It's great to be taught (or schooled) by someone who both understands and sees things on a totally different level like you. I and others have noticed anecdotally (but not quantifiably) that both hub motors and the controllers seem to get hotter doing regen at a give torque level compared to motoring but I had always assumed that was because there were more phase amps flowing during regen than the riders was aware of as we tend to be focused on the (much smaller) battery amperage.

 

[Lebowski]

What you want is as much power into the recipient of this power with minimum losses. This means that for the recipient the voltage and current vector have to be in phase (cos phi = 1).

When powering the motor this means FOC, or, the current vector must line up with the BEMF vector.

In regen this means that the current vector must line up with the voltage vector as seen at the output of the controller. This means maximum power into the battery for minimum losses, or max regen efficiency. But because you are no longer FOC when doing this, you will not get maximum braking torque from the current flowing.

But what do you want in regen mode, max braking torque or maximum energy back into the battery with minimal losses ?

 

[Warren]

I have a question for the experts in this discussion. Over on the chevybolt.org forum, there is an endless discussion about the value of regenerative braking on hills.

The test case is an out and back run, including a one mile long mountain descent at the start, and a short loop at the turn around point, to avoid slowing down. The Bolt has great regen, and cruise control. You can zero the trip odometer, and the average speed screens, just like on a CA, and obtain mi/kWh, distance, and average speed readings.

If you set cruise to 55 mph, it will vary less than one mph over any terrain. So the idea is to do one run at 55 mph in cruise control, and then do a second run where you shift into the electronic "Neutral" gear on the descent, allowing the Bolt to reach whatever speed it will hit due to air, and rolling resistance, and drive the remainder of the test at whatever speed will keep the trip average at 55 mph.

Ignoring the difficulty of knowing exactly when to apply power at the bottom of the descent, and how much, to attain the desired 55 mph average speed, can anyone work out the answer as to which will use less energy, by some physics logic, without actually having to perform the experiment?

 

[ZeroEm]

The test case is an out and back run, including a one mile long mountain descent at the start, and a short loop at the turn around point, to avoid slowing down. The Bolt has great regen, and cruise control. You can zero the trip odometer, and the average speed screens, just like on a CA, and obtain mi/kWh, distance, and average speed readings.

Just my option: Anyone who discusses regen and want's to start out at the top of the hill with guessing a fully charged battery has an AXE to grind. Unless you suggest a one way and start out with a 70% charged battery. Need to put that recovered energy somewhere.

Do the same test but start out at the bottom of the hill and do a round trip.

 

[donn]

In this case it doesn't seem to matter that it starts high - I don't see any braking in the story, so no regen, right?

 

[Warren]

The Bolt does not use the hydraulic brakes at all in cruise control. Speed is maintained entirely by regen. In normal one pedal driving the Bolt, you never engage the hydraulic brakes. It can regen at over -0.3 G to a stop. Most owners use "hilltop reserve" setting, which charges to ~90% of usable capacity, which itself is about 96% of actual full capacity. The cells never reach 4.2 volts. Our brake pads are like brand new after 34K miles of mountainous driving.

 

[serious_sam]

can anyone work out the answer as to which will use less energy, by some physics logic, without actually having to perform the experiment?

The answer would primarily depend on the gradient of the hill, and the coefficient of drag of the vehicle.

 

[ZeroEm]

Have a leaf and if charged to high the regen will not be active. It may be low enough to be active but charging rates on a almost full battery is low so could not handle high charge rates from a down hill run. I don't get everyone's fixation on charging with Regen. Discussion on the trade offs with wind resistance vs regen is a non starter. Any thing that is driven slower uses less energy. Don't need to run the numbers, you can let wind resistance and brake friction hold you back or let you motor charge the battery and slow you down. Which battery will have more amp hrs in it as long it has room to store the charge. If you want more recovery go slower or is this a race, races burn lots of fuel.

 

[serious_sam]

None of you have actually read Warren's post correctly. It's not asking if regen works. It's not specifying a full or empty battery. And you're missing the part about equal average speed for the comparisons.

The trade-off being discussed is this:
1. In one scenario you run slower down the hill at 55mph, and recover some regen, but the you have to maintain that same speed back up the hill (to keep the total average of 55mph), burning lots of power.
2. In the othe scenario, you freewheel down the hill fast, and recover no regen, but because you went much faster than 55mph, you can go much slower back up the hill to maintain the same average speed of 55mph. So you burn less power going back up compared to the previous run.

So the question is "which uses more energy" overall.

I suggest moving this topic to a new thead, since it is a slight divergence and not about ebikes. It is a good topic to discuss though.

 

[Warren]

So the question is "which uses more energy" overall.

I suggest moving this topic to a new thead, since it is a slight divergence and not about ebikes. It is a good topic to discuss though.

Thank you. You get it.

I was hoping to get a short, definitive answer. I am pretty sure I can match or beat any of the former ICE hyper-milers on the Bolt forum just driving in cruise. And as ZeroEm said, dropping the cruise by 1 mph will swamp any advantage coasting down hills may have.

I have an engineer friend who, last year, put seven early Leaf modules in his golf cart, to replace the lead acid batteries. He swapped in a D&D 42A hi-torque motor, SPM-48225 controller, 5 amp onboard charger, and Cycle Analyst. It is 298 lbs lighter. He bottom balanced the cells, and charges to 57.0 volts. On his first full run he did 16.27 miles total, 40.38 Ah, 2,134 Wh, 131 Wh/mi, 7 mph av, 20 mph max, mostly on paths up and down in their woods.

After he did that I got to wondering how efficient the Bolt would be at golf cart speeds.

Turns out the Bolt will do 24 mph on cruise control. You can only get it to engage down to 25 mph. But once in cruise, you can use the minus button to get it to go 24 mph. I did it on a section of the Skyline Drive. I did 11 miles up and 11 miles back, from the south entrance. Overcast, calm, low-to-mid 70's F. Rode with the window rolled down, eating kettle corn, and drinking a soda. It never varied from 24 mph. Saw under 3 mi/kWh on steep climbs, and up to 24 mi/kWh on descents.

Here is the section with elevation per Google.

https://www.google.com/maps/dir/38.1344694,-78.7852796/38.0398414,-78.8524349/@38.0889517,-78.8759985,12z/data=!4m2!4m1!3e1?hl=en

The 3600 pound Bolt averaged 113.6 Wh/mile!

 

[serious_sam]

I was hoping to get a short, definitive answer.

I could do the maths, but like I said, the answer could swing either way, depending on the gradient, the coefficient of friction of the vehicle, and also I forgot to mention, the mass of the vehicle.

For examples:

a) Consider the extreme case that the vehicle's terminal velocity down the hill was 55mph, then both cases would use identical energy, because both maintain 55mph for the entire journey, and neither uses regen.

b) If the drag was very low and terminal velocity high, then both vehicles would use similar energy going back up the hill (drag is a small proportion of the total required energy to ascend), but the vehicle using regen has more at the start of the ascent, so would use less in total.

c) If the drag is high but the mass is very high, then the although the regen vehicle gains energy from the descent, the high drag is a significant proportion of energy required for the ascent, and the lower ascending speed of the freewheel vehicle means it uses less power overall.

If I had to guess, I would say the regen car would use less overall.

 

[John in CR]

So the question is "which uses more energy" overall.

The answer is it depends:
Assuming no use mechanical brakes for either and no significant extra tire friction going around curves coming down fast, then which is more efficient will depend upon how fast you go coasting down with no regen along with the wind resistance of the car and how efficient regen is, because with the same average speed going fast and going slow has more loss to wind resistance than will going a constant speed, since wind resistance increases geometrically. The offset though is that gravity is 100% efficient and regen braking is not. Losses like bearing and rolling resistance increase linearly, so variable or constant speed makes no difference.

My guess would be that the aerodynamics of the car is pretty good, and the linear drags slowing the car while coasting down are significant enough, that the losses in the regen system exceed the extra losses from going faster for part of the trip, so using regen to achieve a constant round trip speed would be less efficient overall.

Mass of the vehicle makes no difference at all, because ignoring the effects of wind resistance and how weight affects rolling resistance it requires the same amount of work to lift the car to a certain height and you recover the same exact amount going down.

 

[ZeroEm]

Sorry, Warren did not understand your question. Always see people think of regen as not useful and load questions to diminish the results. When people try to gain a lot by using Regen they will always be disappointed. The idea is to use less energy and the best way is not to use it in the first place not by trying to recover it. slowing down and using less regen is better than going fast and trying to recover some energy used. You have a good question will need to give it more thought but tests would be better.

 

[qwerkus]

Sorry, Warren did not understand your question. Always see people think of regen as not useful and load questions to diminish the results. When people try to gain a lot by using Regen they will always be disappointed. The idea is to use less energy and the best way is not to use it in the first place not by trying to recover it. slowing down and using less regen is better than going fast and trying to recover some energy used. You have a good question will need to give it more thought but tests would be better.

Seems to me that stored kinetic energy is irrelevant on a bike because of its low system weight. What ppl try to recover is gravitational energy when going down hill, since no matter how slow you climb up, the amount of energy lost/stored this way will always be the same.

 

[Warren]

Thank you all for responding. The comments, as I expected, have been more helpful already than all the bloviating on the Bolt forum.

 

[ZeroEm]

qwerkus, yes bikes are very light compared to a car or truck. I ride with some very light carbon bikes, compare my trike with me on it is over 300lbs, the things I notice is; when we first hit a hill they slow down first and I almost pass them after that and during the hill I need to really power on to keep up with them. Topping the hill and riding down need light regen or brakes so not to pass them. To be fair going down hill my trike is more Aerodynamic may not be the weight, When we first hit a hill I think it is the momentum at first then moves in to carrying the weight up hill. Now do I recover the extra power used to keep up with them. I figure maybe 5% of it.

 

[serious_sam]

Thank you all for responding.

So I did the calculations.

Varying the mass and drag has an affect on the results, but since those specific values are available for the Bolt, I used them in the analysis.

The remaining major variables are the regen efficiency, and the gradient.

Assuming that the regen is about 80% efficient on average (direct conversion of mechanical work at the motor to stored energy in the battery), the theoretical answer is:
- Below 300ft elevation change over the mile, the vehicle can't achieve the 55mph average (without increasing speed up the hill to gain lost time, killing efficiency, and defeating the purpose of the comparison).
- Between 300ft and ~750ft, the coasting vehicle is slightly more efficient (11% max difference).
- Above ~750ft, the regen vehicle becomes more efficient, although 750ft over a mile is very steep (14%), and not so common in many places, so I think not fair to use in the comparison.

This is the energy comparison:

This is the road profile, and velocity for each vehicle for the 750ft (~225m) elevation run:


Sorry about the mixed units. The original problem was posted in freedom units, but the analysis was done in metric, so you get a bit of both back...

So in theory, and under these conditions, the coasting vehicle is very slightly more efficient.

But in real life it probably doesn't make any noticeable difference, and there would be more variation in driving conditions than there would be between the two results.

 

[Warren]

So I did the calculations.

So in theory, and under these conditions, the coasting vehicle is very slightly more efficient.

But in real life it probably doesn't make any noticeable difference, and there would be more variation in driving conditions than there would be between the two results.

Thanks. This was my guess. Nice to see math to back it up. :thumb: