Mounting your battery, Center of Gravity.

[Tiberius]

A leaning bike pivots on its wheels.

John,

I have to say that I wonder at your motivation in this thread. You continually post things like this, and incorrect interpretations of CG, in the face of careful explanations to the opposite.

I don't know whether you really do believe this, or whether you are just doing it to wind safe up.

Nick

 

[John in CR]

Only if you aren't moving. It pivots at the CG with any speed, guaranteed....

Johnrob,

In your words, wrong wrong wrong. During countersteer the rider's weight generally shifts position relative to the bicycle, and the roll behavior (using the term loosely, though I disagree) of the bike frame is centered at an axis lower than CG. Then once the imbalance is created the "fall" starts, which occurs with the contact patches as the axis. Yes there's a transition period where both are taking place, but the fall typically takes place until the deepest part of the curve where gravity and centrifugal force reach an equilibrium. This is a typical turn on a bike, and the equivalent on a motorcycle might be lazily carving the curves on a winding mountain road, which is significantly different than the stronger countersteer of road racing to set up the ideal position throughout the curve and in order to maximize speed.

Just take your bike out and ride it around, and do some lazy turns so you can feel the "fall". Then come back and try to tell me it's only rolling around an axis at the CG. The difference in typical turning on a bike vs a motorcycle is due to the concentration of mass much higher on a bike, and the significant influence of the rider's position change relative to the frame. This makes it an efficient method of turning a bike, which uses very little countersteer.

BTW, weaving the bike back and forth under you is just countersteering, not turning, so of course you're not going to let the fall in the direction of the turn start. Of course there are different degrees of both methods of turning being used depending upon the rider and conditions, but the idea that everything always occurring in an axis around the CG "guaranteed" is inaccurate.

John

 

[John in CR]

A leaning bike pivots on its wheels.

John,

I have to say that I wonder at your motivation in this thread. You continually post things like this, and incorrect interpretations of CG, in the face of careful explanations to the opposite.

I don't know whether you really do believe this, or whether you are just doing it to wind safe up.

Nick

Not at all. You guys are wrong on this point and keep pressing it. I mean you can't even get CG right, so how are you going to get balancing the thing motion right when weight it added in different locations? eg Johnrob still thinks that adding weight extremely low is going to require a far greater lean, when if you place it low enough it won't affect lean angle at all.

John

 

[johnrobholmes]

Uhg, again I am sucked into an argument with no end.


Sure, change perspective to the person and bike shifting around the contact point. Fact is that the center of gravity is still the point of reference for lean angle and turn radius. The roll axis is at the CG, it cannot be lower or higher or else the vector forces of a turn cannot be defined.


Countersteering on a bike IS turning. Weaving back and forth is a perfect example of how a bike handles. Whether the turn is completed or not does not change the fact that the roll axis is centered upon the CG. Whether in a lazy turn or sharp turn, the CG is still the center of the roll axis AND the proper point of reference for the turn- physics does not change with speed. While my body may be falling and the bike coming from underneath me when I initiate a turn (and one could interpret this as pivoting on the contact patch) EVERYTHING involved is rotating around CG.


Of course this is much easier for me to just feel than explain. The CG is the reference point for all movement of any body, whether it have four wheels, four feet, four moons, or two wheels. You are just refusing to take this viewpoint for some reason.



So John, have you tried placing weight low on a bike yet? I have, and it made the lean angles greater. Same bike, same weight, lower CG, higher lean angles, and slower steering from a decentralized mass. How can placing weight "low enough" change this?

 

[Tiberius]

Not at all. You guys are wrong on this point and keep pressing it.

Oh, I've long ago given up pressing it. I'm just fascinated that something that has been so comprehensively explained is still being debated.

Nick

 

[John in CR]

John,

I'm a bit iffy about your lower CG requiring more lean angle in a turn. I understand a high CG bike is inherently more stable, but that's a different issue. Based on your lean angle position, then recumbent low racers would need to get incredibly low in turns, but I'm not sure that's the case. Note that this doesn't change my position that added weight at the contact patches will have zero effect on lean angle.

Now if you want to open your mind to something new. Next time riding, go ahead and do some slight weaving with just countersteer, and then follow through on one of those weaves and "fall" into a real turn.

Regarding your tested placement, it wasn't low enough was too far forward. Placement anywhere of significant weight can be felt in some fashion, and it's great that you tried some different things and shared, though I wouldn't consider it proof of anything.


Tiberius,

I'm not sure what you think has been comprehensively explained. I'm the only one I see doing any explaining. Sure some explanations have been posted, but the idea that anything regarding bicycle behavior has been comprehensively explained is laughable.

John

 

[johnrobholmes]

Testing is proof of nothing, of course. Low recumbents do require more lean angle compared to a higher bike.

We have already been through this. Remember my first post in this thread where I stated that choppers require more lean angle because of lower CG? You almost had an ahah! moment from that, so I will repost it.

Center of Gravity not Center of Mass. With tires on the ground, add weight at rear contact patch changes nothing in the movement of the frame other than dragging the added weight along with you.
John

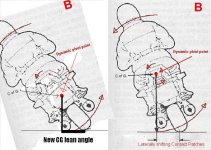
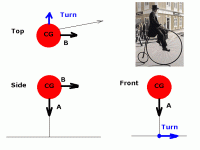
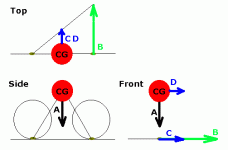
When stationary, the bike would be easy to lean to and fro and the added mass (implies weight) would not be noticable. When moving, the lower CoG would make a given turn need a larger lean. Much like how a chopper is lower than a street bike, and requires more lean to turn the same radius at the same speed. I can offer no math nor science here, only my own experience. I moved my batteries all around on my version two bike, since I didn't need to pedal there was no place I could not move them. I found out that the lower I mounted the packs the worse my handling got as speed increased, I needed more and more lean for the same turns- not safe for the tires I use. I do ride with speed, not walking pace. The best position was in the middle of the bike frame, with weight as high as my own CoG. This made the bike handle more or less the same no matter how many packs I put on. The lean angles didn't change with more weight, my effort to countersteer didn't change with more weight. It was as if the CoG stayed the same and my contact patch merely pivoted underneath to keep myself and the bike balance. At super low speeds (1 or 2mph) the increased weight was noticeable in the middle of the bike, I could feel the momentum of the packs swing around the rear contact patch. I would MUCH prefer a bike that handles well at speed instead of at walking pace. I ride, not walk my bikes.


For this reason I mounted my batteries around the top tube on v3. I constructed them to not interfere with my pedaling, and the weight centered around the top tube is as close to my belly button as possible. It also balances the bike the bike front to rear, which is top priority for having a bike handle well in sketchy conditions. Offroad, low traction, snow, and any tire slipping situation is not a problem with my current setup. The worst setup I can imagine has all of the weight on either front or rear contact patch. If one tire looses traction it is almost impossible to recover.


As an experiment, change your seat height. The lower you put your seat, the more you have to lean to execute a turn at a given speed.

 

[safe]

A Comment

This is why I'm doing a class.

By beginning at the beginning and moving through all the developments that bicycles have gone through the class will cover everything.

Let's skip arguments based on emotion and turn instead to arguments based on science.

In the case of "John in CR" he has no strong physics background to draw upon, so a classroom environment will build up the knowledge base so that if we still disagree in the end at least we all are working with the same laws of physics.

 

[John in CR]

Testing is proof of nothing, of course. Low recumbents do require more lean angle compared to a higher bike.

We have already been through this. Remember my first post in this thread where I stated that choppers require more lean angle because of lower CG? You almost had an ahah! moment from that, so I will repost it.

I'll just go with you on the low CG and lean angle, like I have been, without fully understanding the reason. It doesn't change my position that as you get very low, the placement of added mass has less influence on CG, and at the contact patch none at all. That's not to say it can't be felt, just only when you force it to move laterally.

One of the bikes I'm working on will be fed with heavy lead and nicad batteries, and since it will be a load hauler with racks below the rear axle, I'll be able to experiment with all kinds of different battery placements and report back with results once rainy season winds down in a month or so. Something that might skew my results is that I've extended the wheelbase by 15" ala Xtracycle and Worldbike, so I may need help extrapolating it to meaning on a normal bike. I haven't figured out anything I like to get my split pack mounted below the chainstays on my main bike, which is in the middle of conversion to 2wd.

BTW I wasn't trying to knock your results, just that the sample placements weren't extreme enough for me to reach any conclusion wrt the stuff I'm talking about. It did confirm that low up front makes things sluggish, something I've taken for granted since an early first poster mentioned it some time back.

John

 

[John in CR]

Safe,

You better stick to Scientology because you're shooting blanks when it comes to applied science.

John

 

[johnrobholmes]

Not to be an ass, but really you can't mount your batteries at the contact patch. Your entire argument is based on a fantasy. But, for the sake of education....

The lower you mount a specific mass, the more it will affect and lower CG. Once you get your packs built try this test. Mount them high and near your own CG - take a right turn, followed by a quick left turn. Do the same with the packs mounted low. It will take longer to transfer the weight from right to left since the mass is not centralized, and you will also find that you have to lean more for the same speed and radius of turn.

To test the theory of lower CG taking more lean to turn, just go a specific MPH and turn radius. Then lower your seatpost as much as possible and see if you can feel the difference. I used Safe's diagram to show why you must lean more. The tires must be on the outside of the CG during a turn to keep the rider in balance. Directly under CG is the point of equilibrium. Thus, with lower CG the rider must lean more to keep the CG over the point of equilibrium. Not sure if this is the technically correct way to describe it, but it is how I understand it. My 23 years of riding two wheeled vehicles and recent year of battery pack placement testing coincides with this idea.

 

[John in CR]

Do you and Safe honestly think you can teach? I've understood your point from the beginning. It is wrong, and the graphic you posted proves my most recent point, that a turn is comprised of both. On a bicycle most turns aren't set up with nearly as much countersteer as the motorcycle pictured. You got your A & B backwards. Your B results from countersteer, then the fall starts, which completes the lean and occurs (as pictured by your own graphic as A) as a rotation around the tire. On a typical bike the countersteer results in less lean, so "falling into the turn" starts sooner. This is because the CG is much higher.

I use the rear contact patch only as an example to help those with blinders on see what they refuse to accept, and that is the lower the weight it placed the less is affects CG.

BTW, height of CG has no effect on lean angle other than to the small extent of tire width affects lean angle, and can therefore be ignored for bicycles. "lean angle is unequivocally established as a function of speed and radius of the turn. The height of the CoG is NOT involved in that physical reality." I'm not sure the source of the bias in your observations to the contrary, but they are inaccurate.

Thanks for the graphic though. I was looking for something with bicycles that shows exactly what yours does, and that is display that rotation does in fact occur around the tires as lean continues after countersteer.

John

 

[johnrobholmes]

Since you want to nitpick I will update the drawing. It doesn't matter if it is motorcycle or bicycle, they are all the same (the difference in handling you speak of is the CG). Go add your imaginary weight to the contact patch and have fun. I will spend my time riding and building instead of wasting more time in this thread.

 

[johnrobholmes]

The lower the weight (is) placed the less (it) affects CG.

John

I just had to quote this. Pure golden nuggets here folks :lol:

 

[John in CR]

The lower the weight (is) placed the less (it) affects CG.
John

I just had to quote this. Pure golden nuggets here folks :lol:

Coming from a guy who insisted lean angle is dependent upon height of CG (but it isn't), and who "guaranteed" a bike rolls only around its CG but later posts a graphic to the contrary, your wise cracks mean exactly squat. At some point before this is all settled, I'll prove the above point too. Who knows, maybe you'll even post a graphic proving it for me, so I don't have to do any research.

John

 

[safe]

Turning the High Wheel Bike

First let's see some "exciting scenes" from our last episode. In the last episode the rider has been pitched over the front of the bike because the High Wheel Bike is inherently unstable during braking. We saw this action scene:

In this episode we are going to look at turning the High Wheel Bike. Looking at the picture we see study the "Top View" and see a diagonal thin black line which represents the path that the front wheel would diverge in order to countersteer to set up a lean. The blue line is the corresponding vector that would be the force acting perpendicular to the bikes straight line path. If you need to flip back to vectors and study what they do now is a good time to do it. If need be I'll add another diagram where we get into the traction aspect alone, but I'll skip that one if every understands this. What's tricky is to realize that the traction acts at a distance underneath the CG of the "Top View" and not directly on the CG. The "Front View" gives you a clearer picture, but they actually work together... that's what's great about Orthographic Drawings in that they can represent difficult to communicate ideas fairly easily.

Finally, if you look at the "Front View" picture you see how the turning force will cause a rotation about the Center of Gravity (CG).

This diagram of turning is slightly simplified because in reality the High Wheel Bike had their CG slightly behind the front wheel, but for simplicity sake this is a good approximation.

Please... let's hear some questions or some arguments now about why this might be wrong. You never know, maybe I've made an error already.

 

[safe]

Discussion

The first thing to observe is that on the High Wheel Bike if we assume that the CG is a tightly compressed mass and that the CG is perfectly centered over the front wheel (both being over simplifications of even the High Wheel Bike) then we learn something very important:

"The High Wheel Bike produces 'perfect' countersteer because 100% of the turning force (caused by 100% of the rider weight) produces rotation about the CG. In effect the High Wheel Bike is a unicycle."

...no other bike can make this claim because as you move the CG back and downward you introduce complexities that detract from countersteer. This is the "perfect case" of a pure countersteer machine.

Just don't try to put on the brakes. :lol:

 

[safe]

Traction

The "short answer" for traction is that it's typically no more than the weight that is pressed on the tire, so the easy answer is the coefficient of friction is equal to one. The "long answer" can be found here:

http://en.wikipedia.org/wiki/Coefficient_of_friction

Frequent mistake

Occasionally it is maintained that µ is always < 1, but this is not true. While in most relevant applications µ < 1, a value above 1 merely implies that the force required to slide an object along the surface is greater than the normal force of the surface on the object. For example, silicone rubber or acrylic rubber-coated surfaces have a coefficient of friction that can be substantially larger than 1.

For our purposes assuming that traction equals the weight of our CG as it presses on the ground is "good enough".

This will be important later on... so remember that in order to get a turning force you need weight on the tire... no weight, no turning force... :wink:

 

[John in CR]

Safe,

Since you won't focus your arguments to my 2 primary points, you concede them, so stop the ridiculous flood behind which you are trying to hide your lack of fundamental understanding of how a bike behaves.

John

 

[safe]

The Fundamentals

We have to start from the beginning.

If we don't start from the beginning and cover all the bases then it would be possible to say something like:

"You can't jump from this conclusion to the next, there's no way to make that jump."

...by being patient and meticulous it will make it impossible to avoid the conclusion. Also, just making sure that the physics is covered using vectors and adding the use of orthographic drawings means that there's no more ambiguity in the discussion. It's pretty much impossible to argue with an orthographic drawing.

 

[safe]

Pop Quiz

First one with the correct answer gets "double bonus points". (whatever they are)

Question: In the orthographic diagram the rider is at the very beginning of the turn sequence. What is the ultimate goal for the rider... which direction does he plan to go and so in which direction is he planning to lean?

(this is easy for those following the countersteer discussions)

 

[safe]

Traction Available

As was discussed in a previous episode, the amount of traction that is available to a tire at it's contact point is directly related to the amount of the weight of the bike/rider unit that is directly over that tire. So in the case of the "High Wheel Bicycle" you have all of your weight over the front tire and that means that all of the traction that is theoretically possible can be used.

What happens when you move the weight back... how does traction on the front tire change?


Let's be clear we are NOT yet talking about handling as in the way the bike feels or how easily or difficult it is to turn but the ABSOLUTE quantity of traction that we are dealing with before the tire let's go and skids.

The answer is simple... as the weight of the bike/rider unit is moved to the rear you get less and less traction on the front wheel. If you were to get all the weight over the rear and none at all in the middle or front there would be no traction on the front tire, so if you turned the front wheel sideways it would skid along like you were riding on ice.

I'm not done debunking the "rear weight bike" because there are other reasons why it doesn't work, but for the moment this is the first of the reasons that it can't work.

If all the weight is on the rear end the front tire gets no traction!

(we might call this "strike one")

 

[safe]

The "Safety Bike"

Let's review just a little. The High Wheel Bike was absolute perfection when it came to countersteer because 100% of the weight of the bike/rider was over the front wheel giving it maximum traction and responsiveness in turning. Had this been all that mattered we would all be riding High Wheel Bikes. The problem with the High Wheel Bike is that since all the weight is forward they tip over the front end when you use the brakes. That's so dysfunctional that it's a non-starter for practical use and so something new had to be developed.

By 1885 we get the first "Safety Bicycle" which moved the Center of Gravity backwards to near the middle of the bike:

We now create an orthographic drawing to represent the "Safety Bike" and include the contact patches. It's at the contact patches that force vectors act.


Okay, now it starts to get interesting because we will apply the force vector at the front tire contact patch ("B" in Green) and we then see that this force vector ends up effecting the Center of Gravity in two ways:


"C" - The "C" vector represents the rotational torque that the Center of Gravity experiences about it's rotational axis. The actual effective axis is complex because the rear wheel is not rigidly attached to the ground. At zero mph the rear contact patch is fixed, but at higher speed the rear wheel will drift outward more easily thus changing the "apparent" rotational axis. Luckily this doesn't effect our discussion now because we just want to be able to say that a "C" vector exists and that it has some value.

"D" - At zero mph the "D" vector is the strongest because at zero mph the rear contact patch is stationary. A stationary rear contact patch means that the Center of Gravity is actually being moved off line of the straight line path. This is very important because it means that the desired countersteer behavior is being made worse. (the bike's Center of Gravity is being sent off in the wrong direction ) To know what this vector is we would need to know how much rotational inertia the bike/rider unit actually had. In a sense this vector is the "sluggishness" tendency of the bike. (less rotational inertia means less of this vector)

Summary

The "Safety Bike" helps to resolve the problem that the "High Wheel Bike" had about braking. However, now we introduce new problems where the Center of Gravity has a new force vector to deal with. Fix one problem and you can sometimes cause another. So the "Safety Bike" is a compromise design.

 

[safe]

Wrapping Our Minds Around the "D" Vector

What does this "D" vector mean to us as we ride a bike?

The "D" vector represents the Center of Gravity actually being forced off line from the straight line path. This means that if you are going really fast and enter a turn upright and need to generate countersteer to prepare a lean to go to the RIGHT then you need to do like the diagram shows and turn to the LEFT (what it means to do countersteer) and that will produce two vectors "C" and "D" that will prepare you for that turn. We haven't even begun to turn yet... we are still trying to get the damn bike leaned over... and it's fighting what we want to do because the Center of Gravity of the bike is being directed to the LEFT.

We want to go RIGHT and the Center of Gravity is being sent LEFT !!!

...this is insane. But it's the effect you get from this "D" vector. This is why it's so important to get the rotational mass as tightly concentrated along the axis of rotation because the more spread out the overall mass the more extreme this "D" vector becomes.

Is everyone following this? Questions?

 

[Tiberius]

safe,

forgive me, but this is all utter bollocks.

I pointed out when John in CR had got things wrong, so its only fair that I point out that all this stuff about traction and vectors is wrong.

Nick