Motor comparison spreadsheet

[speedmd]

Yes, temperature drive$ the boat as they say, in so many ways. Some sort of dissipation coefficient calculus is needed. Motor Mass is big part as you stated John, surface area another. External cooling fins, good heat path from stator iron, vent holes, fins and fans, liquid cooling etc etc... We should be able to come up with some good values for a few of the motors and compare to test data for correlations. Some designs are just better in this regard and the better designed motors (all else being equal) can take much more abuse and output longer in hostile conditions. Even if it was a simple / gross percentage de-rating we can assign to power curves for those motors less able to cool themselves.

 

[Miles]

Unfortunately Rm goes up about 4X.

Come on John. Keep up...

 

[Miles]

Yes a factor for heat dissipation for different motor types was something Justin suggested in the initial thread.

 

[John in CR]

Yes a factor for heat dissipation for different motor types was something Justin suggested in the initial thread.

It can be so variable with conditions that a reliable number or coefficient will be tough. A fill in the blank number in watts could still be quite useful.

 

[John in CR]

Unfortunately Rm goes up about 4X.

Come on John. Keep up...

Got me not paying full attention. Double the lamination stack is definitely 1/2 the Kv (double the Kt), and Rm doubles except the end winding portion, which is unchanged.

What's it do to hysteresis and eddy current losses? It seems like they'd simply double too.

 

[Miles]

What's it do to hysteresis and eddy current losses? It seems like they'd simply double too.

Yes.

 

[Punx0r]

I did a basic exercise in Excel based on the Turnigy 80-100 motor with multiples of stack length from 1 to 20 with the Kv, Kt and Rm scaled proportionatly. Mass was also scaled by simple multiple, although I accept this isn't entirely realistic.

"Ideal" Km is simply Km for 1 x stack length kept constant.

Of the results some are linear, some non-linear, but all progressively diverge from ideal except for sKm^2 (but not Km^2).

Hope this might be of some interest. I have a feeling I should repeat the exercise for motors in parallel (so the weight multiplier is accurate), but I suspect the answers will be the same.

 

[crossbreak]

all progressively diverge from ideal except for sKm^2 (but not Km^2).

your cals seem to be ok. i dont get what ideal Km shall be good for?
we replaced sKm by sKm² in his spreadsheet since this is more useful for comparison. Km² with the unit [Nm] and sKm² with the unit [Nm/kg]

 

[Miles]

Thanks PunxOr

Nio surprises. That's what we would expect to see...

 

[John in CR]

Still trying to make a not so good number better? You'll know your getting somewhere when the comparison shows HubMonster and MidMonster to be virtually identical. They're the same design, same stator steel, poles, slots, etc. One is just a bit larger and wound to a higher Kv. Using mass as part of computation could be misleading, since that assumes they both have the same % of unnecessary weight.

 

[Miles]

Still trying to make a not so good number better? You'll know your getting somewhere when the comparison shows HubMonster and MidMonster to be virtually identical. They're the same design, same stator steel, poles, slots, etc. One is just a bit larger and wound to a higher Kv. Using mass as part of computation could be misleading, since that assumes they both have the same % of unnecessary weight.

Using mass isn't misleading at all. The actual values for your motors, in the spreadsheet, seem to be what one would expect.....

 

[crossbreak]

i agree, miles. a motor having lower sKm² doesn't have to be bad. it may just be small in diameter.
Just have a look at the DD hubs. They all get great sKm² figures, but we all know that they are not necessarily the pride of creation. Again we find that core loss may not be neglected

 

[Miles]

Some motors are optimised for torque density, some for power density. Also, larger motors have the advantage over smaller ones....

 

[John in CR]

Still trying to make a not so good number better? You'll know your getting somewhere when the comparison shows HubMonster and MidMonster to be virtually identical. They're the same design, same stator steel, poles, slots, etc. One is just a bit larger and wound to a higher Kv. Using mass as part of computation could be misleading, since that assumes they both have the same % of unnecessary weight.

Using mass isn't misleading at all. The actual values for your motors, in the spreadsheet, seem to be what one would expect.....

I meant only as a test of the new number we, actually you guys, come up with. The 2 motors should have a virtually identical "motor constant", and if they don't then the number needs more work AFAIC. The one part the two may be different is in the % unnecessary weight. At some point I'll mod a HubMonster for mid-drive use. I have a MidMonster almost ready and fully trimmed. With both well trimmed in rotor weight, then they should be a good test of any number.

 

[Miles]

Obviously, the motor constant won't be the same, either as Km or Km². That's why we divide by mass. Dividing by mass and using the "idealised" figures that PunxOr did, sKm² is indeed constant.

You shouldn't necessarily expect the same sKm² figures for your two motors because larger motors have something of an advantage, as I said. There could be other reasons, too. Differences in non essential mass, that you mentioned; inaccuracies of measurement etc.

It seems to work as expected. The results reflect the measurements you took...

 

[Punx0r]

Sorry, that "ideal" Km was a mistake. It should have been sKm, showing how sKm *should* remain constant as the stack is lengthened (or motors put in parallel).

I will correct it.

 

[John in CR]

Obviously, the motor constant won't be the same, either as Km or Km². That's why we divide by mass. Dividing by mass and using the "idealised" figures that PunxOr did, sKm² is indeed constant.

You shouldn't necessarily expect the same sKm² figures for your two motors because larger motors have something of an advantage, as I said. There could be other reasons, too. Differences in non essential mass, that you mentioned; inaccuracies of measurement etc.

It seems to work as expected. The results reflect the measurements you took...

That's just scaling the same motor by lengthening the stator, but a good and valid number should scale in all ways. Km simply isn't the number, and neither will be squaring it or dividing by mass. Like Luke said "It is was it is", to which I'll add "and that's not a number worthy of being called the "motor constant".

 

[Miles]

Sure, it doesn't account for everything but it's a dose of reality to counter the subjective drivel we usually get.

 

[crossbreak]

As a rule of thumb, you could say that a Km² of 30+ is needed to climb hills like 20% with a total vehicle mass of 150kg and a 26" wheel: This means 100Nm at the wheel with efficiency in the upper 70s

A Km² of 17, like HubMonster has, is not enough. It would need a tire that is 25% smaller or a 1.33 reduction to a 26" wheel. ( 17 * 1.33² = 30)

Looking at the RV120, it would be a quite nice hill climber, it gets a Km² of 41.7 at a reduction ratio of 5:1

two Bafang BPM together get 27.6, not bad either

miles simulated inrunner gets 30.4 at 5:1 reduction amazing for such a tiny motor! you did a nice job!

 

[Punx0r]

Data and graph updated in previous post. I also tried it with motors wired in parallel and the results are identical. If nothing else I now finally understand what's previously been said

If Km is a relative indication of the output a motor is capable of then it makes sense that twice as much motor (or two identical motors) should have double the Km value and the same specific-Km. Km^2 does achieve that. However it really does only demonstrate torque-generating efficiency (torque output per watt). I think it's a traditional view that with electric motors they are primarily torque machines, "you pay for torque" - meaning if you want torque it required more active material, more motor, hence the idea of comparing motors on something other than physical size of the casing.

The idea of a motor constant perhaps makes more sense when comparing different sized motors that of fundamentally similar construction, like 3 phase mains induction motors, which are likely to be made of the same materials and have similar efficiencies and thermal properties.

I agree that Km or Km^2 isn't the whole story, but it's a start. You preach yourself the idea of "volt up, gear down" to get more power from a motor. The torque output is fairly fixed, but extra power can be had almost for free by speeding it up - till core losses come and ruin the party. I guess there you've got specific-power (Km^2/mass x power) x efficiency (either total for the motor or for core loss alone). That might tell us how good a motor is at converting electricity to output power, but doesn't tell us anything about thermal issues.

 

[John in CR]

As a rule of thumb, you could say that a Km² of 30+ is needed to climb hills like 20% with a total vehicle mass of 150kg and a 26" wheel: This means 100Nm at the wheel with efficiency in the upper 70s

A Km² of 17, like HubMonster has, is not enough. It would need a tire that is 25% smaller or a 1.33 reduction to a 26" wheel. ( 17 * 1.33² = 30)

Looking at the RV120, it would be a quite nice hill climber, it gets a Km² of 41.7 at a reduction ratio of 5:1

two Bafang BPM together get 27.6, not bad either

miles simulated inrunner gets 30.4 at 5:1 reduction amazing for such a tiny motor! you did a nice job!

So much for your rule of thumb. Pushing an all up load of over 190kg, not only can HubMonster climb a solid 20% grade, but the sharp blind curves made me slow to quite low speeds and then I accelerated to up to 80kph on the straights that were long enough.

FWIW Hillsofvalp had his on a dyno running significantly higher current than I do, and he still managed 67% efficiency at peak power, which included all losses (controllers, tire, etc). I run significantly higher voltage, but lower current, so on my install efficiency at peak power will be significantly higher than 67%, quite possibly a bit over 80%. Comparing Hubmonster to 2 BPMs or even a Revolt 120 is a bad joke.

 

[Miles]

miles simulated inrunner gets 30.4 at 5:1 reduction amazing for such a tiny motor! you did a nice job!

I make it 11.2.....

 

[crossbreak]

Comparing Hubmonster to 2 BPMs or even a Revolt 120 is a bad joke.

no it's math. I built so many middrives, that i think i can say that i have experience with this. This isn't just math, it's reality, i²R loss is the major factor when climbing hills.
For example, I like climbing technical passages of single trails with my 26" MTB, at a speed of roughly 10-15kph, lots of obstacles, roots, rocks, this is what I enjoy.

pushing a 150kg load a 20% hill at, say 14.4 kph (4m/s) need P=gain*velocity*mass*g = 0.2*4m/s*150kg*10m/s² =1200W of power at 100Nm of torque for climbing the hill, not taking any drag into account

At 100Nm, Hubmonster has a loss of I²R = (T/Kt)² * Rm = (100/0.522)²*.016Ω = 587W of copper loss alone, efficiency = 1200W/(1200+587W) =67%

Two Bafang BPM:
I²R = (T/Kt)² * Rm = (100/ .982)²*.035Ω = 363W loss, efficiency = 1200W/(1200+363W) = 77%

this is not surprising at all, since two Bafang BPM are technically larger than a single Hubmonster. They simply have larger Km²

Miles, remember that Km² for a drive is (Km*reduction)². We had this already. So this is (1.1*5)²=30 for your 120mm inrunner, 11.2:1 reduction would be a complete overkill, except you wanna emigrate to india and built a monster rickshaw to become a rich man EDIT: Got the wrong Rm figure here

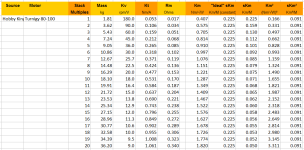
For comparison: Some column with i²R loss at 100Nm show what a reduction drive can do with i²R loss This is the simple reason why middrives are so awesome hill climbers

 

[Miles]

Oh, I see what it is.. Somehow, you've got the wrong figure for Rm.... It should be 0.166 Ohms. That's what I have in my spreadsheet.

Too much cutting and pasting..

 

[crossbreak]

ups, corrected. you need a reduction of 8.3:1 to get a Km² of 30